2022年吉林中考数学真题及答案
数学试题共6页,包括六道大题,共26道小题;全卷满分120分。考试时间120分钟;考试结束后,将本试题和答题卡一并交回
注意事项:
1.答题前,请您将自己的姓名、准考证号填写在答题卡上,并将条形码准确粘贴在条形码区域内
2.答题时,请按照考试要求在答题卡上的指定区域内作答,在草稿纸、试题上答题无效
一、单项选择题(每小题2分,共12分)
1. 吉林松花石有“石中之宝”的美誉,用它制作的砚台叫松花砚,能与中国四大名砚媲美.下图是一款松花砚的示意图,其俯视图为( )

A.  B.
B.  C.
C.  D.
D. 
【答案】C
【解析】
【分析】根据俯视图的定义(从上面观察物体所得到的视图)即可得.
【详解】解:其俯视图是由两个同心圆(不含圆心)组成,即为
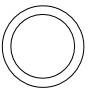 ,
,
故选:C.
【点睛】本题考查了俯视图,熟记定义是解题关键.
2. 要使算式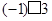 的运算结果最大,则“□”内应填入的运算符号为( )
的运算结果最大,则“□”内应填入的运算符号为( )
A. + B. - C. × D. ÷
【答案】A
【解析】
【分析】将各选项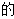 运算符号代入计算即可得.
运算符号代入计算即可得.
【详解】解: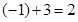 ,
,
 ,
,
 ,
,
 ,
,
因为 ,
,
所以要使运算结果最大,应填入的运算符号为 ,
,
故选:A.
【点睛】本题考查有理数的加减乘除运算,熟练掌握运算法则是解题关键.
3. 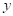 与2的差不大于0,用不等式表示为( )
与2的差不大于0,用不等式表示为( )
A. 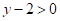 B.
B. 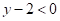 C.
C.  D.
D. 
【答案】D
【解析】
【分析】根据差运算、不大于的定义列出不等式即可.
【详解】解:由题意,用不等式表示为 ,
,
故选:D.
【点睛】本题考查了列一元一次不等式,熟练掌握“不大于是指小于或等于”是解题关键.
4. 实数 ,
,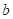 在数轴上对应点的位置如图所示,则
在数轴上对应点的位置如图所示,则 ,
,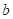 的大小关系为( )
的大小关系为( )

A. 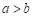 B.
B. 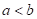 C.
C.  D. 无法确定
D. 无法确定
【答案】B
【解析】
【分析】在以向右为正方向的数轴上,右边的点表示的数大于左边的点表示的数,根据此结论即可得出结论.
【详解】由图知,数轴上数b表示的点在数a表示的点的右边,则b>a
故选:B.
【点睛】本题考查了数轴上有理数大小的比较,是基础题.
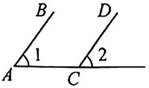
5. 如图,如果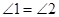 ,那么
,那么 ,其依据可以简单说成( )
,其依据可以简单说成( )
A 两直线平行,内错角相等 B. 内错角相等,两直线平行
两直线平行,内错角相等 B. 内错角相等,两直线平行
C. 两直线平行,同位角相等 D. 同位角相等,两直线平行
【答案】D
【解析】
【分析】根据“同位角相等,两直线平行”即可得.
【详解】解:因为 与
与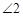 是一对相等的同位角,得出结论是
是一对相等的同位角,得出结论是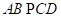 ,
,
所以其依据可以简单说成同位角相等,两直线平行,
故选:D.
【点睛】本题考查了平行线的判定,熟练掌握平行线的判定方法是解题关键.
6. 如图,在 中,
中,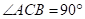 ,
,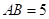 ,
,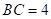 .以点
.以点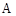 为圆心,
为圆心,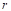 为半径作圆,当点
为半径作圆,当点 在
在 内且点
内且点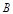 在
在 外时,
外时,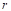 的值可能是( )
的值可能是( )

A. 2 B. 3 C. 4 D. 5
【答案】C
【解析】
【分析】先利用勾股定理可得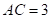 ,再根据“点
,再根据“点 在
在 内且点
内且点 在
在 外”可得
外”可得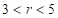 ,由此即可得出答案.
,由此即可得出答案.
【详解】解: 在
在 中,
中,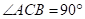 ,
,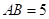 ,
,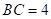 ,
,
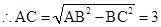 ,
,
 点
点 在
在 内且点
内且点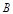 在
在 外,
外,
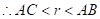 ,即
,即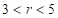 ,
,
观察四个选项可知,只有选项C符合,
故选:C.
【点睛】本题考查了勾股定理、点与圆的位置关系,熟练掌握点与圆的位置关系是解题关键.
二、填空题(每小题3分,共24分)
7. 实数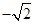 的相反数是__________.
的相反数是__________.
【答案】
【解析】
【分析】根据只有符号不同的两个数为互为相反数进行解答.
【详解】解:根据相反数 定义,
定义,
可得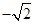 的相反数是
的相反数是 .
.
故答案为:
【点睛】此题主要考查了实数的性质,关键是掌握相反数的定义.
8. 计算: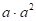 =____.
=____.
【答案】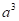
【解析】
【详解】试题分析:根据同底数幂的乘法性质,底数不变,指数相加,可直接结算,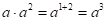 .
.
考点:同底数幂的乘法
9. 篮球队要购买10个篮球,每个篮球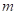 元,一共需要__________元.(用含
元,一共需要__________元.(用含 的代数式表示)
的代数式表示)
【答案】
【解析】
【分析】根据“总费用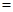 购买篮球的数量
购买篮球的数量 每个篮球的价格”即可得.
每个篮球的价格”即可得.
【详解】解:由题意得:一共需要的费用为 元,
元,
故答案为: .
.
【点睛】本题考查了列代数式,正确找出等量关系是解题关键.
10. 《九章算术》中记载了一道数学问题,其译文为:有大小两种盛酒的桶,已知5个大桶加上1个小桶可以盛酒3斛(斛,音hú,是古代一种容量单位),1个大桶加上5个小桶可以盛酒2斛.1个大桶、1个小桶分别可以盛酒多少斛?设1个大桶可以盛酒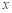 斛、1个小桶可以盛酒
斛、1个小桶可以盛酒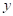 斛.根据题意,可列方程组为__________.
斛.根据题意,可列方程组为__________.
【答案】 ##
##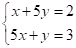
【解析】
【分析】根据题中两个等量关系:5个大桶加上1个小桶可以盛酒3斛;1个大桶加上5个小桶可以盛酒2斛,列出方程组即可.
【详解】由题意得: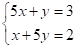
故答案为: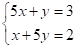 .
.
【点睛】本题考查了列二元一次方程组解实际问题,理解题意、找到等量关系并列出方程组是解题的关键.
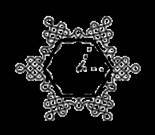
11. 第二十四届北京冬奥会入场式引导牌上的图案融入了中国结和雪花两种元素.如图,这个图案绕着它的中心旋转角 后能够与它本身重合,则角
后能够与它本身重合,则角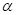 可以为__________度.(写出一个即可)
可以为__________度.(写出一个即可)
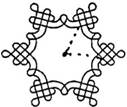
【答案】60或120或180或240或300(写出一个即可)
【解析】
【分析】如图(见解析),求出图中正六边形的中心角,再根据旋转的定义即可得.
【详解】解:这个图案对应着如图所示的一个正六边形,它的中心角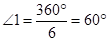 ,
,
 ,
,
 角
角 可以为
可以为 或
或 或
或 或
或 或
或 ,
,
故答案 :60或120或180或240或300(写出一个即可).
:60或120或180或240或300(写出一个即可).
【点睛】本题考查了正多边形的中心角、图形的旋转,熟练掌握正多边形的性质是解题关键.
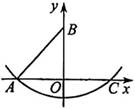
12. 如图,在平面直角坐标系中,点 的坐标为
的坐标为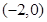 ,点
,点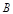 在
在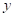 轴正半轴上,以点
轴正半轴上,以点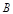 为圆心,
为圆心,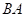 长为半径作弧,交
长为半径作弧,交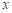 轴正半轴于点
轴正半轴于点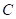 ,则点
,则点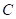 的坐标为__________.
的坐标为__________.
【答案】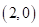
【解析】
【分析】连接 ,先根据点
,先根据点 的坐标可得
的坐标可得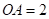 ,再根据等腰三角形的判定可得
,再根据等腰三角形的判定可得 是等腰三角形,然后根据等腰三角形的三线合一可得
是等腰三角形,然后根据等腰三角形的三线合一可得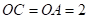 ,由此即可得出答案.
,由此即可得出答案.
【详解】解:如图,连接 ,
,

 点
点 的坐标为
的坐标为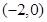 ,
,
 ,
,
由同圆半径相等得: ,
,
 是等腰三角形,
是等腰三角形,
 ,
,
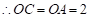 (等腰三角形的三线合一),
(等腰三角形的三线合一),
又 点
点 位于
位于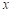 轴正半轴,
轴正半轴,
 点
点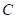 的坐标为
的坐标为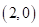 ,
,
故答案为: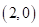 .
.
【点睛】本题考查了同圆半径相等、等腰三角形的三线合一、点坐标等知识点,熟练掌握等腰三角形的三线合一是解题关键.
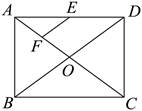
13. 如图,在矩形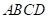 中,对角线
中,对角线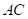 ,
,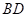 相交于点
相交于点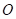 ,点
,点 是边
是边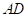 的中点,点
的中点,点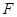 在对角线
在对角线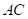 上,且
上,且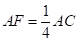 ,连接
,连接 .若
.若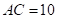 ,则
,则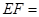 __________.
__________.
【答案】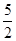 ##2.5
##2.5
【解析】
【分析】由矩形的性质可得点F是OA的中点,从而EF是△AOD的中位线,则由三角形中位线定理即可求得EF的长.
【详解】∵四边形ABCD是矩形,
∴BD=AC=10,OA= AC,OD=
AC,OD= BD=5,
BD=5,
∵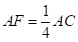 ,
,
∴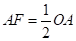 ,即点F是OA的中点.
,即点F是OA的中点.
∵点 是边
是边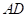 的中点,
的中点,
∴EF是△AOD的中位线,
∴ .
.
故答案为: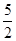 .
.
【点睛】本题考查了矩形的性质,三角形中位线定理等知识,掌握中位线定理是本题的关键.
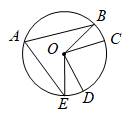
14. 如图,在半径为1的 上顺次取点
上顺次取点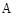 ,
,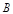 ,
, ,
, ,
, ,连接
,连接 ,
, ,
, ,
, ,
, ,
, .若
.若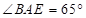 ,
, ,则
,则 与
与 的长度之和为__________.(结果保留
的长度之和为__________.(结果保留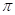 ).
).
【答案】 ##
##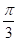
【解析】
【分析】由圆周角定理得 ,根据弧长公式分别计算出
,根据弧长公式分别计算出 与
与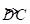 的长度,相减即可得到答案.
的长度,相减即可得到答案.
【详解】解:∵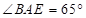 ,
,
∴
又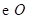 的半径为1,
的半径为1,
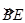 的长度=
的长度=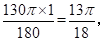
又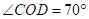 ,
,
∴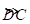 的长度=
的长度=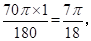
∴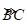 与
与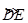 的长度之和=
的长度之和= ,
,
故答案为: .
.
【点睛】本题主要考查了计算弧长,圆周角定理,熟练掌握弧长计算公式是解答本题的关键.
三、解答题(每小题5分,共20分)
15. 如图,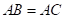 ,
, .求证:
.求证: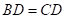 .
.
【答案】证明见解析
【解析】
【分析】先利用三角形全等的判定定理( 定理)证出
定理)证出 ,再根据全等三角形的性质即可得.
,再根据全等三角形的性质即可得.
【详解】证明:在 和
和 中,
中,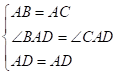 ,
,
 ,
,
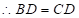 .
.
【点睛】本题考查了三角形全等的判定与性质,熟练掌握三角形全等的判定与性质是解题关键.
16. 下面是一道例题及其解答过程的一部分,其中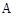 是关于
是关于 的多项式.请写出多项式
的多项式.请写出多项式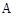 ,并将该例题的解答过程补充完整.
,并将该例题的解答过程补充完整.
例先去括号,再合并同类项: 解:
|
【答案】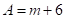 ,解答过程补充完整为
,解答过程补充完整为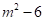
【解析】
【分析】利用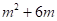 除以
除以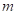 可得
可得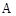 ,再根据合并同类项法则补充解答过程即可.
,再根据合并同类项法则补充解答过程即可.
【详解】解:观察第一步可知,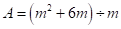 ,
,
解得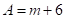 ,
,
将该例题的解答过程补充完整如下: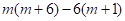

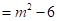 ,
,
故答案为: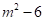 .
.
【点睛】本题考查了多项式的乘除法、合并同类项,熟练掌握整式的运算法则是解题关键.
17. 长白山国家级自然保护区、松花湖风景区和净月潭国家森林公园是吉林省著名的三个景区.甲、乙两人用抽卡片的方式决定一个自己要去的景区.他们准备了3张不透明的卡片,正面分别写上长白山、松花湖、净月潭.卡片除正面景区名称不同外其余均相同,将3张卡片正面向下洗匀,甲先从中随机抽取一张卡片,记下景区名称后正面向下放回,洗匀后乙再从中随机抽取一张卡片,请用画树状图或列表的方法,求两人都决定去长白山的概率.
【答案】甲、乙两人都决定去长白山的概率为 .
.
【解析】
【分析】画树状图,共有9种等可能的结果,其中两人都决定去长白山的结果有1种,再由概率公式求解即可.
【详解】解:长白山、松花湖、净月潭依次用字母A,B,C表示,
画树状图如下:

共有9种等可能的结果,其中甲、乙两人都决定去长白山的结果有1种,
∴甲、乙两人都决定去长白山的概率为 .
.
【点睛】此题考查的是用树状图法求概率以及随机事件等知识.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.
18. 图①,图②均是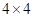 的正方形网格,每个小正方形的顶点称为格点.其中点
的正方形网格,每个小正方形的顶点称为格点.其中点 ,
, ,
, 均在格点上.请在给定的网格中按要求画四边形.
均在格点上.请在给定的网格中按要求画四边形.
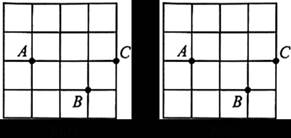
(1)在图①中,找一格点 ,使以点
,使以点 ,
, ,
, ,
, 为顶点的四边形是轴对称图形;
为顶点的四边形是轴对称图形;
(2)在图②中,找一格点 ,使以点
,使以点 ,
, ,
, ,
, 为顶点的四边形是中心对称图形.
为顶点的四边形是中心对称图形.
【答案】(1)图见解析
(2)图见解析
【解析】
【分析】(1)以 所在直线为对称轴,找出点
所在直线为对称轴,找出点 的对称点即为点
的对称点即为点 ,再顺次连接点
,再顺次连接点 即可得;
即可得;
(2)根据点 平移至点
平移至点 的方式,将点
的方式,将点 进行平移即可得点
进行平移即可得点 ,再顺次连接点
,再顺次连接点 即可得.
即可得.
【小问1详解】
解:如图①,四边形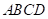 是轴对称图形.
是轴对称图形.
 【小问2详解】
【小问2详解】
解:先将点 向左平移2格,再向上平移1个可得到点
向左平移2格,再向上平移1个可得到点 ,
,
则将点 按照同样的平移方式可得到点
按照同样的平移方式可得到点 ,
,
如图②,平行四边形 是中心对称图形.
是中心对称图形.
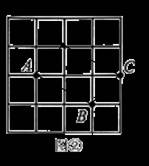
【点睛】本题考查了轴对称图形与中心对称图形、平移作图,熟练掌握轴对称图形与中心对称图形的概念是解题关键.
四、解答题(每小题7分,共28分)
19. 刘芳和李婷进行跳绳比赛.已知刘芳每分钟比李婷多跳20个,刘芳跳135个所用的时间与李婷跳120个所用的时间相等.求李婷每分钟跳绳的个数.
【答案】160个
【解析】
【分析】设李婷每分钟跳绳的个数为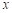 个,则刘芳每分钟跳绳的个数为
个,则刘芳每分钟跳绳的个数为 个,根据“刘芳跳135个所用的时间与李婷跳120个所用的时间相等”建立方程,解方程即可得.
个,根据“刘芳跳135个所用的时间与李婷跳120个所用的时间相等”建立方程,解方程即可得.
【详解】解:设李婷每分钟跳绳的个数为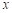 个,则刘芳每分钟跳绳的个数为
个,则刘芳每分钟跳绳的个数为 个,
个,
由题意得: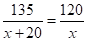 ,
,
解得 ,
,
经检验, 是所列分式方程的解,且符合题意,
是所列分式方程的解,且符合题意,
答:李婷每分钟跳绳的个数为160个.
【点睛】本题考查了分式方程的实际应用,正确找出等量关系,并建立方程是解题关键.
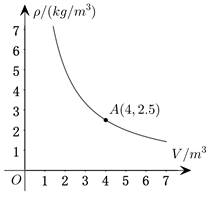
20. 密闭容器内有一定质量的气体,当容器的体积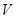 (单位:
(单位: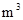 )变化时,气体的密度
)变化时,气体的密度 (单位:
(单位: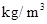 )随之变化.已知密度
)随之变化.已知密度 与体积
与体积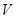 是反比例函数关系,它的图像如图所示.
是反比例函数关系,它的图像如图所示.
(1)求密度 关于体积
关于体积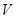 的函数解析式;
的函数解析式;
(2)当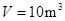 时,求该气体的密度
时,求该气体的密度 .
.
【答案】(1)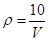
(2)1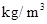
【解析】
【分析】(1)用待定系数法即可完成;
(2)把V=10值代入(1)所求得的解析式中,即可求得该气体的密度.
【小问1详解】
设密度 关于体积
关于体积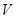 的函数解析式为
的函数解析式为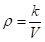 ,
,
把点A的坐标代入上式中得: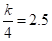 ,
,
解得:k=10,
∴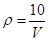 .
.
【小问2详解】
当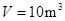 时,
时,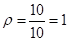 (
(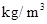 ).
).
即此时该气体的密度为1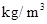 .
.
【点睛】本题是反比例函数的应用问题,考查了求反比例函数的解析式及求反比例函数的函数值等知识,由图像求得反比例函数解析式是关键.
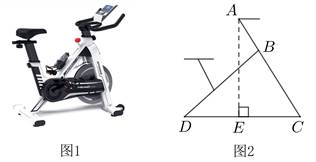
21. 动感单车是一种新型的运动器械.图①是一辆动感单车的实物图,图②是其侧面示意图.△BCD为主车架,AB为调节管,点A,B,C在同一直线上.已知BC长为70cm,∠BCD的度数为58°.当AB长度调至34cm时,求点A到CD的距离AE的长度(结果精确到1cm).(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)
【答案】点A到CD的距离AE的长度约为88cm.
【解析】
【分析】根据正弦的概念即可求解.
【详解】解:在Rt△ACE中,∠AEC=90°,∠ACE=58°,AC=AB+BC=34+70=104(cm),
∵sin∠ACE=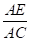 ,即sin58°=
,即sin58°=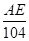 ,
,
∴AE=104×0.85=88.4≈88(cm),
∴点A到CD的距离AE的长度约为88cm.
【点睛】本题考查的是解直角三角形的知识,掌握锐角三角函数的概念是解题的关键.
22. 为了解全国常住人口城镇化率的情况,张明查阅相关资料,整理数据并绘制统计图如下:
2017-2021年年末全国常住人口城镇化率城化率
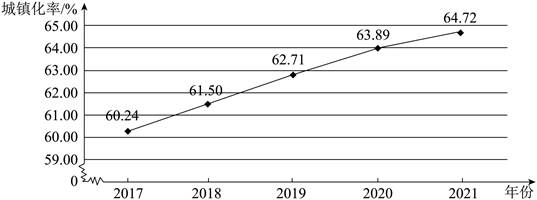
(以上数据来源于《中华人民共和国2021年国民经济和社会发展统计公报》)
注: .例如,城镇常住人口60.12万人,总人口100万人,则总人口城镇化率为60.12%.
.例如,城镇常住人口60.12万人,总人口100万人,则总人口城镇化率为60.12%.
回答下列问题:
(1)2017-2021年年末,全国常住人口城镇化率的中位数是 %;
(2)2021年年末全国人口141260万人,2021年年末全国城镇常住人口为 万人;(只填算式,不计算结果)
(3)下列推断较为合理的是 (填序号).
①2017-2021年年末,全国常住人口城镇化率逐年上升,估计2022年年末全国常住人口城镇化率高于64.72%.
②全国常住人口城镇化率2020年年末比2019年年末增加1.18%,2021年年末比2020年年末增加0.83%,全国常住人口城镇化率增加幅度减小,估计2022年年末全国常住人口城镇化率低于64.72%.
【答案】(1)
(2)
(3)①
【解析】
【分析】(1)根据中位数的定义即可得;
(2)根据城镇化率的计算公式即可得;
(3)根据全国常住人口城镇化率逐年上升的趋势,可估计2022年年末全国常住人口城镇化率高于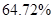 ,由此即可得出答案.
,由此即可得出答案.
【小问1详解】
解:2017-2021年年末,全国常住人口城镇化率按从小到大进行排序为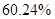 ,
, ,
,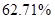 ,
,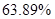 ,
,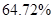 ,则排在中间位置的数即为中位数,
,则排在中间位置的数即为中位数,
所以中位数为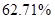 ,
,
故答案为: .
.
【小问2详解】
解:2021年年末全国城镇常住人口为 万人,
万人,
故答案为: .
.
【小问3详解】
解:2017-2021年年末,全国常住人口城镇化率逐年上升,估计2022年年末全国常住人口城镇化率高于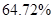 ,则推断①较为合理;
,则推断①较为合理;
全国常住人口城镇化率2020年年末比2019年年末增加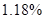 ,2021年年末比2020年年末增加
,2021年年末比2020年年末增加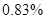 ,全国常住人口城镇化率增加幅度减小,可估计全国常住人口城镇化率2022年年末比2021年年末增加幅度小于
,全国常住人口城镇化率增加幅度减小,可估计全国常住人口城镇化率2022年年末比2021年年末增加幅度小于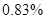 ,但2022年年末全国常住人口城镇化率会高于
,但2022年年末全国常住人口城镇化率会高于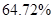 ,则推断②不合理;
,则推断②不合理;
故答案为:①.
【点睛】本题考查了中位数和折线统计图,读懂折线统计图是解题关键.
五、解答题(每小题8分,共16分)
23. 李强用甲、乙两种具有恒温功能的热水壶同时加热相同质量的水,甲壶比乙壶加热速度快.在一段时间内,水温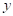 (℃)与加热时间
(℃)与加热时间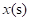 之间近似满足一次函数关系,根据记录的数据,画函数图象如下:
之间近似满足一次函数关系,根据记录的数据,画函数图象如下:
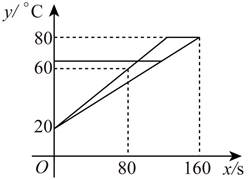
(1)加热前水温是 ℃;
(2)求乙壶中水温 关于加热时间
关于加热时间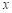 的函数解析式;
的函数解析式;
(3)当甲壶中水温刚达到80℃时,乙壶中水温是 ℃.
【答案】(1)20 (2)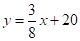
(3)65
【解析】
【分析】(1)根据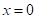 时,
时,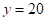 即可得;
即可得;
(2)先判断出乙壶对应的函数图象经过点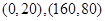 ,再利用待定系数法即可得;
,再利用待定系数法即可得;
(3)先利用待定系数法求出甲壶中 与
与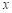 的函数解析式,再求出
的函数解析式,再求出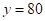 时,
时,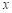 的值,然后将
的值,然后将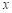 的值代入乙壶中
的值代入乙壶中 与
与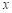 的函数解析式即可得.
的函数解析式即可得.
【小问1详解】
解:由函数图象可知,当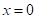 时,
时,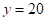 ,
,
则加热前水温是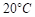 ,
,
故答案为:20.
【小问2详解】
解:因为甲壶比乙壶加热速度快,
所以乙壶对应的函数图象经过点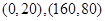 ,
,
设乙壶中水温 关于加热时间
关于加热时间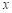 的函数解析式为
的函数解析式为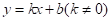 ,
,
将点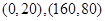 代入得:
代入得: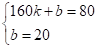 ,
,
解得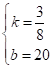 ,
,
则乙壶中水温 关于加热时间
关于加热时间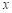 的函数解析式为
的函数解析式为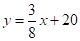 .
.
【小问3详解】
解:设甲壶中水温 关于加热时间
关于加热时间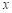 的函数解析式为
的函数解析式为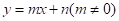 ,
,
将点 代入得:
代入得: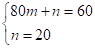 ,
,
解得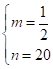 ,
,
则甲壶中水温 关于加热时间
关于加热时间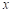 的函数解析式为
的函数解析式为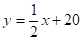 ,
,
当 时,
时, ,解得
,解得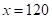 ,
,
将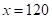 代入
代入 得:
得: ,
,
即当甲壶中水温刚达到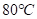 时,乙壶中水温是
时,乙壶中水温是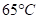 ,
,
故答案为:65.
【点睛】本题考查了一次函数的实际应用,读懂函数图象,并熟练掌握待定系数法是解题关键.
24. 下面是王倩同学的作业及自主探究笔记,请认真阅读并补充完整.
【作业】如图①,直线 ,
, 与
与 的面积相等吗?为什么?
的面积相等吗?为什么?
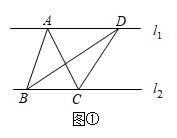
解:相等.理由如下:
设 与
与 之间的距离为
之间的距离为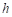 ,则
,则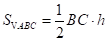 ,
,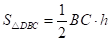 .
.
∴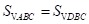 .
.
【探究】
(1)如图②,当点 在
在 ,
, 之间时,设点
之间时,设点 ,
, 到直线
到直线 的距离分别为
的距离分别为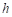 ,
,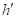 ,则
,则 .
.
证明:∵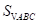
(2)如图③,当点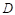 在
在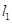 ,
, 之间时,连接
之间时,连接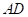 并延长交
并延长交 于点
于点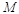 ,则
,则 .
.

证明:过点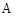 作
作 ,垂足为
,垂足为 ,过点
,过点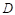 作
作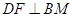 ,垂足为
,垂足为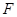 ,则
,则 ,
,
∴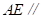 .
.
∴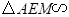 .
.
∴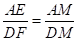 .
.
由【探究】(1)可知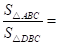 ,
,
∴ .
.
(3)如图④,当点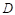 在
在 下方时,连接
下方时,连接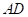 交
交 于点
于点 .若点
.若点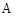 ,
, ,
,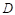 所对应的刻度值分别为5,1.5,0,
所对应的刻度值分别为5,1.5,0,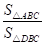 的值为 .
的值为 .

【答案】(1)证明见解析
(2)证明见解析 (3)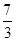
【解析】
【分析】(1)根据三角形的面积公式可得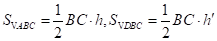 ,由此即可得证;
,由此即可得证;
(2)过点 作
作 ,垂足为
,垂足为 ,过点
,过点 作
作 ,垂足为
,垂足为 ,先根据平行线的判定可得
,先根据平行线的判定可得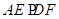 ,再根据相似三角形的判定可证
,再根据相似三角形的判定可证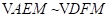 ,根据相似三角形的性质可得
,根据相似三角形的性质可得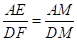 ,然后结合【探究】(1)的结论即可得证;
,然后结合【探究】(1)的结论即可得证;
(3)过点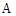 作
作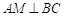 于点
于点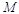 ,过点
,过点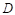 作
作 于点
于点 ,先根据相似三角形的判定证出
,先根据相似三角形的判定证出 ,再根据相似三角形的性质可得
,再根据相似三角形的性质可得 ,然后根据三角形的面积公式可得
,然后根据三角形的面积公式可得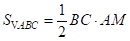 ,
,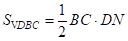 ,由此即可得出答案.
,由此即可得出答案.
【小问1详解】
证明: ,
,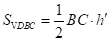 ,
,
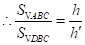 .
.
【小问2详解】
证明:过点 作
作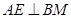 ,垂足为
,垂足为 ,过点
,过点 作
作 ,垂足为
,垂足为 ,则
,则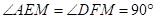 ,
,
 .
.
 .
.
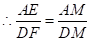 .
.
由【探究】(1)可知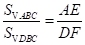 ,
,
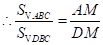 .
.
【小问3详解】
解:过点 作
作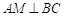 于点
于点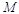 ,过点
,过点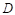 作
作 于点
于点 ,则
,则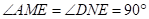 ,
,
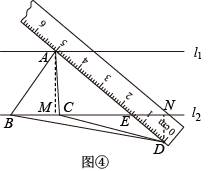
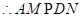 ,
,
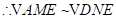 ,
,
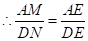 ,
,
 点
点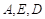 所对应的刻度值分别为5,
所对应的刻度值分别为5, ,0,
,0,
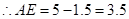 ,
,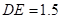 ,
,
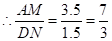 ,
,
又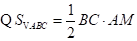 ,
,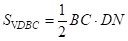 ,
,
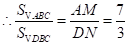 ,
,
故答案为: .
.
【点睛】本题考查了相似三角形的判定与性质、平行线的判定、三角形的面积等知识点,熟练掌握相似三角形的判定与性质是解题关键.
六、解答题(每小题10分,共20分)
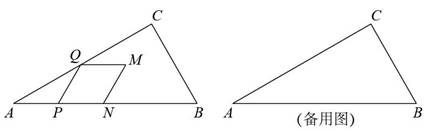
25. 如图,在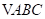 中,
中,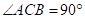 ,
,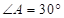 ,
,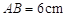 .动点
.动点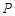 从点
从点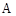 出发,以
出发,以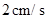 的速度沿边
的速度沿边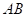 向终点
向终点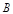 匀速运动.以
匀速运动.以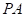 为一边作
为一边作 ,另一边
,另一边 与折线
与折线 相交于点
相交于点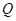 ,以
,以 为边作菱形
为边作菱形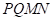 ,点
,点 在线段
在线段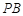 上.设点
上.设点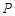 的运动时间为
的运动时间为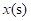 ,菱形
,菱形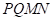 与
与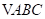 重叠部分图形的面积为
重叠部分图形的面积为 .
.
(1)当点 在边
在边 上时,
上时, 的长为
的长为  ;(用含
;(用含 的代数式表示)
的代数式表示)
(2)当点 落在边
落在边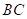 上时,求
上时,求 的值;
的值;
(3)求 关于
关于 的函数解析式,并写出自变量
的函数解析式,并写出自变量 的取值范围.
的取值范围.
【答案】(1)2x (2)1
(3)
【解析】
【分析】(1)先证明∠A=∠AQP=30°,即AP=PQ,根据题意有AP=2x,即PQ=2x;
(2)当M点在BC上,Q点在AC上,在(1)中已求得AP=PQ=2x,再证明△MNB是等边三角形,即有BN=MN,根据AB=6x=6cm,即有x=1(s);
(3)分类讨论:当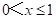 时,此时菱形PQMN在△ABC的内部,此时菱形PQMN与△ABC重叠的面积即是菱形PQMN的面积,过Q点作QG⊥AB于G点,求出菱形的面积即可;当x>1,且Q点在线段AC上时,过Q点作QG⊥AB于G点,设QM交BC于F点,MN交BC于E点,过M点作NH⊥EF于H点,先证明△ENB是等边三角形、△MEF是等边三角形,重叠部分是菱形PQMN的面积减去等边△MEF的面积,求出菱形PQMN的面积和等边△MEF的面积即可,此时需要求出当Q点在C点时的临界条件;当
时,此时菱形PQMN在△ABC的内部,此时菱形PQMN与△ABC重叠的面积即是菱形PQMN的面积,过Q点作QG⊥AB于G点,求出菱形的面积即可;当x>1,且Q点在线段AC上时,过Q点作QG⊥AB于G点,设QM交BC于F点,MN交BC于E点,过M点作NH⊥EF于H点,先证明△ENB是等边三角形、△MEF是等边三角形,重叠部分是菱形PQMN的面积减去等边△MEF的面积,求出菱形PQMN的面积和等边△MEF的面积即可,此时需要求出当Q点在C点时的临界条件;当 时,此时Q点在线段BC上,此时N点始终与B点重合,过Q点作QG⊥AB于G点,重叠部分的面积就是△PBQ的面积,求出等边△PBQ的面积即可.
时,此时Q点在线段BC上,此时N点始终与B点重合,过Q点作QG⊥AB于G点,重叠部分的面积就是△PBQ的面积,求出等边△PBQ的面积即可.
【小问1详解】
当Q点在AC上时,
∵∠A=30°,∠APQ=120°,
∴∠AQP=30°,
∴∠A=∠AQP,
∴AP=PQ,
∵运动速度为每秒2cm,运动时间为x秒,
∴AP=2x,
∴PQ=2x;
【小问2详解】
当M点在BC上,Q点在AC上,如图,
在(1)中已求得AP=PQ=2x,
∵四边形QPMN是菱形,
∴PQ=PN=MN=2x,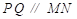 ,
,
∵∠APQ=120°,
∴∠QPB=60°,
∵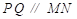 ,
,
∴∠MNB=∠QPB=60°,
∵在Rt△ABC中,∠C=90°,∠A=30°,
∴∠B=60°,
∴△MNB是等边三角形,
∴BN=MN,
∴AB=AP+PN+BN=2x×3=6x=6cm,
∴x=1(s);
【小问3详解】
当P点运动到B点时,用时6÷2=3(s),
即x的取值范围为: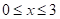 ,
,
当M点刚好在BC上时,
在(2)中已求得此时x=1,
分情况讨论,
即当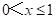 时,此时菱形PQMN在△ABC的内部,
时,此时菱形PQMN在△ABC的内部,
∴此时菱形PQMN与△ABC重叠的面积即是菱形PQMN的面积,
过Q点作QG⊥AB于G点,如图,
∵∠APQ=120°,
∴∠QPN=60°,即菱形PQMN的内角∠QPN=∠QMN=60°,
∴QG=PQ×sin∠QPN=2x×sin60°= ,
,
∴重叠的面积等于菱形PQMN的面积为,

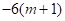 .
.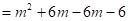
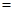 .
.