2022年福建中考数学试题试卷及答案
一、选择题:本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.
1. -11的相反数是( )
A. -11 B. ![]() C.
C. ![]() D. 11
D. 11
【答案】D
2. 如图所示的圆柱,其俯视图是()

A.  B.
B. 
C.  D.
D. 
【答案】A
3. 5G应用在福建省全面铺开,助力千行百业迎“智”变,截止2021年底,全省5G终端用户达1397.6万户,数据13 976 000用科学记数法表示为()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
4. 美术老师布置同学们设计窗花,下列作品为轴对称图形的是( )
A.  B.
B. 
C.  D.
D. 
【答案】A
5. 如图,数轴上的点P表示下列四个无理数中的一个,这个无理数是( )
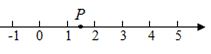
A. ![]() B.
B. ![]() C.
C. ![]() D. π
D. π
【答案】B
6. 不等式组![]() 的解集是( )
的解集是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
7. 化简![]() 的结果是( )
的结果是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
8. 2021年福建省的环境空气质量达标天数位居全国前列,下图是福建省10个地区环境空气质量综合指数统计图.
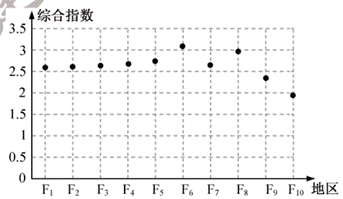
综合指数越小,表示环境空气质量越好.依据综合指数,从图中可知环境空气质量最好的地区是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
9. 如图所示的衣架可以近似看成一个等腰三角形ABC,其中AB=AC,![]() ,BC=44cm,则高AD约为( )(参考数据:
,BC=44cm,则高AD约为( )(参考数据:![]() ,
,![]() ,
,![]() )
)
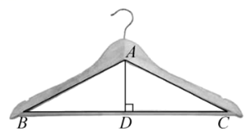
A. 9.90cm B. 11.22cm C. 19.58cm D. 22.44cm
【答案】B
10. 如图,现有一把直尺和一块三角尺,其中![]() ,
,![]() ,AB=8,点A对应直尺的刻度为12.将该三角尺沿着直尺边缘平移,使得△ABC移动到
,AB=8,点A对应直尺的刻度为12.将该三角尺沿着直尺边缘平移,使得△ABC移动到![]() ,点
,点![]() 对应直尺的刻度为0,则四边形
对应直尺的刻度为0,则四边形![]() 的面积是( )
的面积是( )
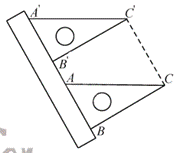
A. 96 B. ![]() C. 192 D.
C. 192 D. ![]()
【答案】B
二、填空题:本题共6小题,每小题4分,共24分.
11. 四边形的外角和等于_______.
【答案】360°.
12. 如图,在△ABC中,D,E分别是AB,AC的中点.若BC=12,则DE的长为______.
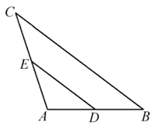
【答案】6
13. 一个不透明的袋中装有3个红球和2个白球,这些球除颜色外无其他差别.现随机从袋中摸出一个球,这个球是红球的概率是______.
【答案】![]()
14. 已知反比例函数![]() 的图象分别位于第二、第四象限,则实数k的值可以是______.(只需写出一个符合条件的实数)
的图象分别位于第二、第四象限,则实数k的值可以是______.(只需写出一个符合条件的实数)
【答案】-5(答案不唯一 负数即可)
15. 推理是数学的基本思维方式、若推理过程不严谨,则推理结果可能产生错误.
例如,有人声称可以证明“任意一个实数都等于0”,并证明如下:
设任意一个实数为x,令![]() ,
,
等式两边都乘以x,得![]() .①
.①
等式两边都减![]() ,得
,得![]() .②
.②
等式两边分别分解因式,得![]() .③
.③
等式两边都除以![]() ,得
,得![]() .④
.④
等式两边都减m,得x=0.⑤
所以任意一个实数都等于0.
以上推理过程中,开始出现错误的那一步对应的序号是______.
【答案】④
16. 已知抛物线![]() 与x轴交于A,B两点,抛物线
与x轴交于A,B两点,抛物线![]() 与x轴交于C,D两点,其中n>0,若AD=2BC,则n的值为______.
与x轴交于C,D两点,其中n>0,若AD=2BC,则n的值为______.
【答案】8
三、解答题:本题共9小题,共86分.解答应写出文字说明、证明过程或演算步骤.
17. 计算:![]() .
.
【答案】![]()
【详解】解:原式![]() .
.
18. 如图,点B,F,C,E在同一条直线上,BF=EC,AB=DE,∠B=∠E.求证:∠A=∠D.

【答案】见解析
【详解】证明:∵BF=EC,
∴![]() ,即BC=EF.
,即BC=EF.
在△ABC和△DEF中,
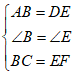 ,
,
∴![]() ,
,
∴∠A=∠D.
19. 先化简,再求值:![]() ,其中
,其中![]() .
.
【答案】![]() ,
,![]() .
.
【详解】解:原式![]()
![]()
![]() .
.
当![]() 时,原式
时,原式![]() .
.
20. 学校开展以“劳动创造美好生活”为主题的系列活动,同学们积极参与主题活动的规划、实施、组织和管理,组成调查组、采购组、规划组等多个研究小组.
调查组设计了一份问卷,并实施两次调查.活动前,调查组随机抽取50名同学,调查他们一周的课外劳动时间t(单位:h),并分组整理,制成如下条形统计图.活动结束一个月后,调查组再次随机抽取50名同学,调查他们一周的课外劳动时间t(单位:h),按同样的分组方法制成如下扇形统计图,其中A组为![]() ,B组为
,B组为![]() ,C组为
,C组为![]() ,D组为
,D组为![]() ,E组为
,E组为![]() ,F组为
,F组为![]() .
.

(1)判断活动前、后两次调查数据的中位数分别落在哪一组;
(2)该校共有2000名学生,请根据活动后的调查结果,估计该校学生一周的课外劳动时间不小于3h的人数.
【答案】(1)活动前调查数据的中位数落在C组;活动后调查数据的中位数落在D组
(2)1400人
【小问1详解】
活动前,一共调查了50名同学,中位数是第25和26个数据的平均数,
∴活动前调查数据的中位数落在C组;
活动后,A、B、C三组的人数为![]() (名),
(名),
D组人数为:![]() (名),15+15=30(名)
(名),15+15=30(名)
活动后一共调查了50名同学,中位数是第25和26个数据的平均数,
∴活动后调查数据的中位数落在D组;
【小问2详解】
一周的课外劳动时间不小于3h的比例为![]() ,
,![]() (人);
(人);
答:根据活动后的调查结果,估计该校学生一周的课外劳动时间不小于3h的人数为1400人.
21. 如图,△ABC内接于⊙O,![]() 交⊙O于点D,
交⊙O于点D,![]() 交BC于点E,交⊙O于点F,连接AF,CF.
交BC于点E,交⊙O于点F,连接AF,CF.
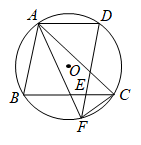
(1)求证:AC=AF;
(2)若⊙O的半径为3,∠CAF=30°,求![]() 的长(结果保留π).
的长(结果保留π).
【答案】(1)见解析(2)![]()
【小问1详解】
∵![]() ,
,![]() ,
,
∴四边形ABED是平行四边形,
∴∠B=∠D.
又∠AFC=∠B,∠ACF=∠D,
∴![]() ,
,
∴AC=AF.
【小问2详解】
连接AO,CO.

由(1)得∠AFC=∠ACF,
又∵∠CAF=30°,
∴![]() ,
,
∴![]() .
.
∴![]() 的长
的长![]() .
.
22. 在学校开展“劳动创造美好生活”主题系列活动中,八年级(1)班负责校园某绿化角的设计、种植与养护.同学们约定每人养护一盆绿植,计划购买绿萝和吊兰两种绿植共46盆,且绿萝盆数不少于吊兰盆数的2倍.已知绿萝每盆9元,吊兰每盆6元.
(1)采购组计划将预算经费390元全部用于购买绿萝和吊兰,问可购买绿萝和吊兰各多少盆?
(2)规划组认为有比390元更省钱的购买方案,请求出购买两种绿植总费用的最小值.
【答案】(1)购买绿萝38盆,吊兰8盆
(2)369元
【小问1详解】
设购买绿萝![]() 盆,购买吊兰
盆,购买吊兰![]() 盆
盆
∵计划购买绿萝和吊兰两种绿植共46盆
∴![]()
∵采购组计划将预算经费390元全部用于购买绿萝和吊兰,绿萝每盆9元,吊兰每盆6元
∴![]()
得方程组![]()
解方程组得![]()
∵38>2×8,符合题意
∴购买绿萝38盆,吊兰8盆;
【小问2详解】
设购买绿萝![]() 盆,购买吊兰吊
盆,购买吊兰吊![]() 盆,总费用为
盆,总费用为![]()
∴![]() ,
,![]()
∴![]()
∵总费用要低于过390元,绿萝盆数不少于吊兰盆数的2倍
∴![]()
将![]() 代入不等式组得
代入不等式组得![]()
∴![]()
∴![]() 的最大值为15
的最大值为15
∵![]() 为一次函数,随
为一次函数,随![]() 值增大而减小
值增大而减小
∴![]() 时,
时,![]() 最小
最小
∴![]()
∴![]() 元
元
故购买两种绿植最少花费为![]() 元.
元.
23. 如图,BD是矩形ABCD的对角线.
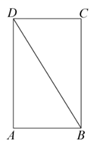
(1)求作⊙A,使得⊙A与BD相切(要求:尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,设BD与⊙A相切于点E,CF⊥BD,垂足为F.若直线CF与⊙A相切于点G,求![]() 的值.
的值.
【答案】(1)作图见解析
(2)![]()
【小问1详解】
解:如图所示,⊙A即为所求作:
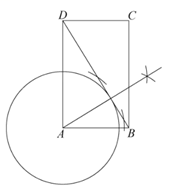 【小问2详解】
【小问2详解】
解:根据题意,作出图形如下:
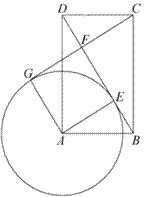
设![]() ,⊙A的半径为r,
,⊙A的半径为r,
∵BD与⊙A相切于点E,CF与⊙A相切于点G,
∴AE⊥BD,AG⊥CG,即∠AEF=∠AGF=90°,
∵CF⊥BD,
∴∠EFG=90°,
∴四边形AEFG是矩形,
又![]() ,
,
∴四边形AEFG是正方形,
∴![]() ,
,
在Rt△AEB和Rt△DAB中,![]() ,
,![]() ,
,
∴![]() ,
,
在Rt△ABE中,![]() ,
,
∴![]() ,
,
∵四边形ABCD是矩形,
∴![]() ,AB=CD,
,AB=CD,
∴![]() ,又
,又![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在Rt△ADE中,![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() ,
,
∵![]() ,
,
∴![]() ,即tan∠ADB的值为
,即tan∠ADB的值为![]() .
.
24. 已知![]() ,AB=AC,AB>BC.
,AB=AC,AB>BC.
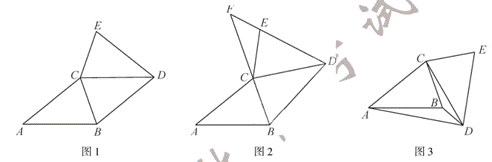
(1)如图1,CB平分∠ACD,求证:四边形ABDC是菱形;
(2)如图2,将(1)中的△CDE绕点C逆时针旋转(旋转角小于∠BAC),BC,DE的延长线相交于点F,用等式表示∠ACE与∠EFC之间的数量关系,并证明;
(3)如图3,将(1)中的△CDE绕点C顺时针旋转(旋转角小于∠ABC),若![]() ,求∠ADB的度数.
,求∠ADB的度数.
【答案】(1)见解析(2)![]() ,见解析
,见解析
(3)30°
【小问1详解】
∵![]() ,
,
∴AC=DC,
∵AB=AC,
∴∠ABC=∠ACB,AB=DC,
∵CB平分∠ACD,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴四边形ABDC是平行四边形,
又∵AB=AC,
∴四边形ABDC是菱形;
【小问2详解】
结论:![]() .
.
证明:∵![]() ,
,
∴![]() ,
,
∵AB=AC,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
【小问3详解】
在AD上取一点M,使得AM=CB,连接BM,
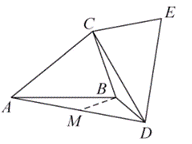
∵AB=CD,![]() ,
,
∴![]() ,
,
∴BM=BD,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,
∵CA=CD,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即∠ADB=30°.
,即∠ADB=30°.
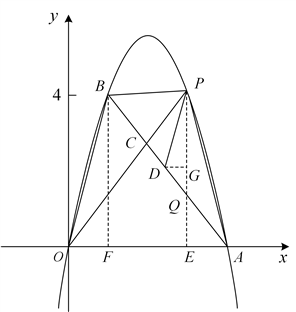
25. 在平面直角坐标系xOy中,已知抛物线![]() 经过A(4,0),B(1,4)两点.P是抛物线上一点,且在直线AB的上方.
经过A(4,0),B(1,4)两点.P是抛物线上一点,且在直线AB的上方.
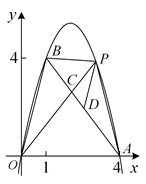
(1)求抛物线的解析式;
(2)若△OAB面积是△PAB面积的2倍,求点P的坐标;
(3)如图,OP交AB于点C,![]() 交AB于点D.记△CDP,△CPB,△CBO的面积分别为
交AB于点D.记△CDP,△CPB,△CBO的面积分别为![]() ,
,![]() ,
,![]() .判断
.判断![]() 是否存在最大值.若存在,求出最大值;若不存在,请说明理由.
是否存在最大值.若存在,求出最大值;若不存在,请说明理由.
【答案】(1)![]()
(2)存在,![]() 或(3,4)
或(3,4)
(3)存在,![]()
【小问1详解】
解:(1)将A(4,0),B(1,4)代入![]() ,
,
得![]() ,
,
解得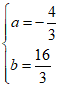 .
.
所以抛物线的解析式为![]() .
.
【小问2详解】
设直线AB的解析式为![]() ,
,
将A(4,0),B(1,4)代入![]() ,
,
得![]() ,
,
解得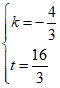 .
.
所以直线AB的解析式为![]() .
.
过点P作PM⊥x轴,垂足为M,PM交AB于点N.
过点B作BE⊥PM,垂足为E.
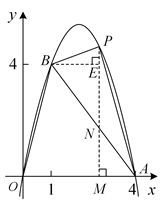
所以![]()
![]()
![]()
![]() .
.
因为A(4,0),B(1,4),所以![]() .
.
因为△OAB的面积是△PAB面积的2倍,
所以![]() ,
,![]() .
.
设![]() ,则
,则![]() .
.
所以![]() ,
,
即![]() ,
,
解得![]() ,
,![]() .
.
所以点P的坐标为![]() 或(3,4).
或(3,4).
【小问3详解】
![]()
![]()
![]()
![]()
记△CDP,△CPB,△CBO的面积分别为![]() ,
,![]() ,
,![]() .则
.则![]()
![]()
如图,过点![]() 分别作
分别作![]() 轴的垂线,垂足分别
轴的垂线,垂足分别![]() ,
,![]() 交
交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 的平行线,交
的平行线,交![]() 于点
于点![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]() ,
,
设![]()
![]() 直线AB的解析式为
直线AB的解析式为![]() .
.
设![]() ,则
,则![]()
![]()
![]()
![]()
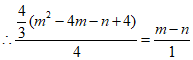
整理得![]()
![]()
![]()
![]()
![]()
![]()
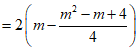
![]()
![]()
![]() 时,
时,![]() 取得最大值,最大值为
取得最大值,最大值为![]()
